免责声明

村长本人对这个东西也是半斤八两，如果有误请友善指出，谢谢。

我学东西有个我认为比较强迫症的地方，就是无论学啥我总是喜欢对这个东西的底层也学会，导致我每学一门课可能就会需要去补一下其他相关的课程，然后这门课的进度就得等我补完之后才能继续，导致我的学习效率比较低下。而且我也比较懒，经常在补其他课程知识的时候就不想学了，然后拖着，导致不仅补的课程没学完，连要学的这门课也基本没怎么学。也是在这种情况下，快要度过自己的学习生涯了。

我对于微积分的浅薄理解

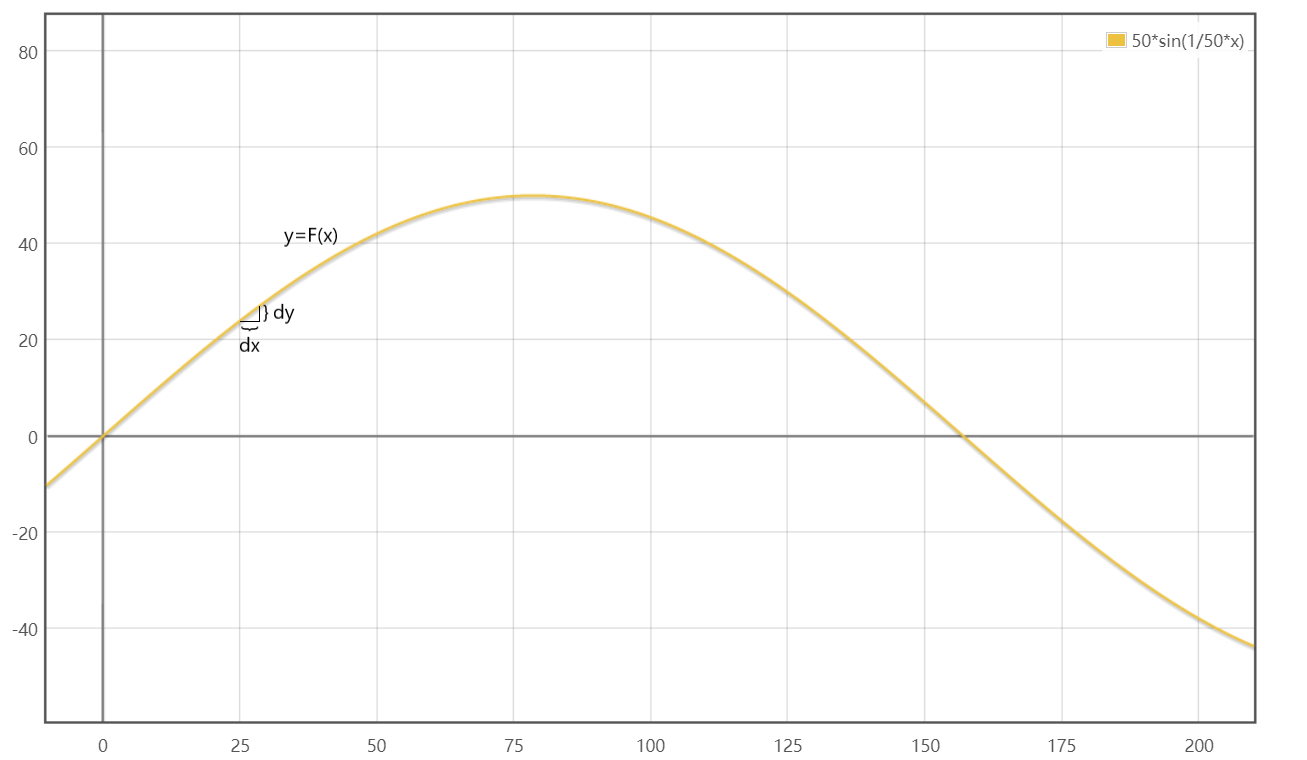
首先，你对一个函数进行求导（如上图），得出来的导函数大概下面是这个图像，因为这个图像呢反应的是原函数斜率变化的一个图像，为啥积分就是求原函数，且听我娓娓道来。

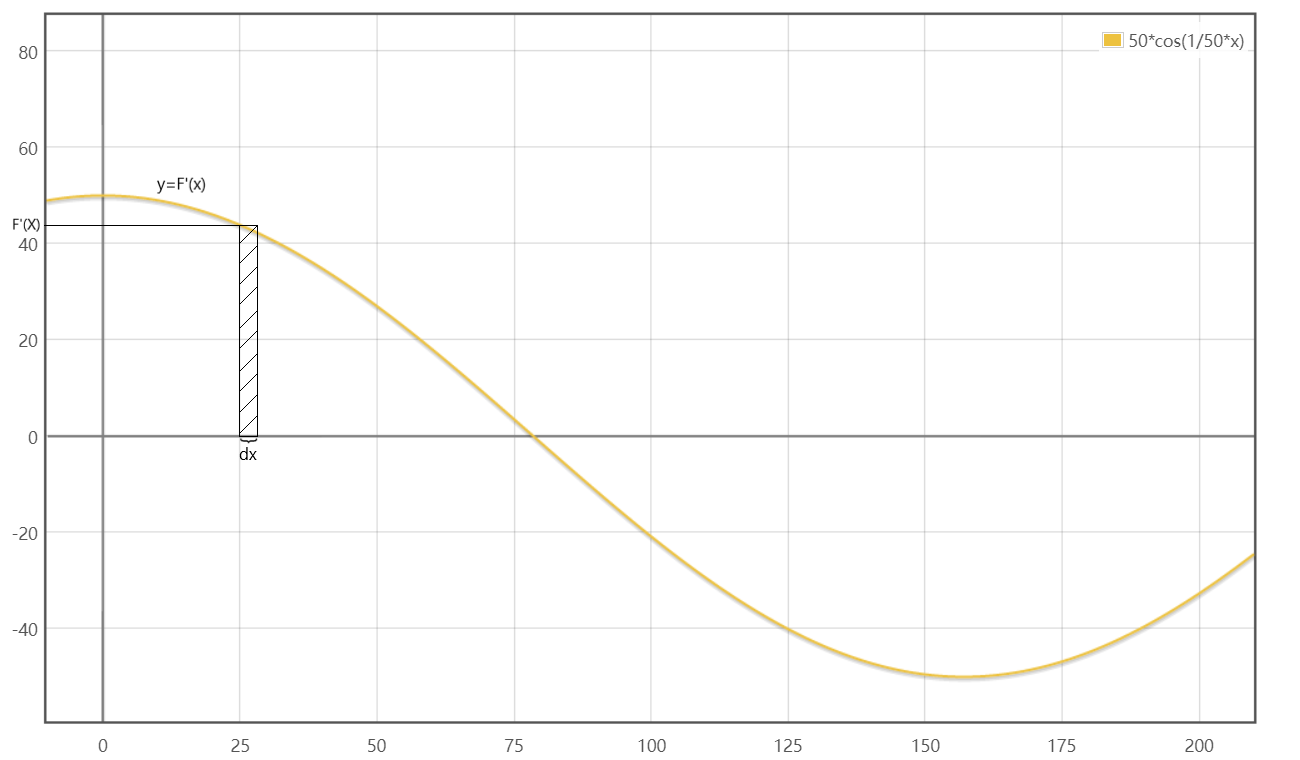
假设现在有一个函数，你要求他的积分，这个积分的本意呢是求的这个函数的面积，因为他不像长方形正方行，底乘高就能得出来面积，他是一个曲面，你得把他分成足够小的一块块面积，然后进行累加，才能得到一个比较精确的结果，这个过程就叫积分，但是如果你真要这么算，这么多小的面积加起来，那你可能很难算出来。

我们假设上面的函数为$F’(x)$，那么他所围成的面积就是$F’(x)dx$，因为本图为最上面那张图的导函数图像，所以在同一位置，它的导数也就是$\frac{dy}{dx} = F’(x)$，而刚才所说要求的积分（也就是面积）$\int F’(x)dx$就等于$\frac{dy}{dx}dx = dy$（微分），结果就是上方函数（也就是原函数）在dx的范围内的y的增量。所以知道为啥两者是互逆的过程了吧。

最后总结一句话，就是你想求的函数的积分（面积），就是要求出其对应原函数的y的增量。